Learning Target: I can define types of angle pairs and use their properties to find missing measurements and solve problems. Learning Target: I can define types of angle pairs and use their properties to find missing measurements and solve problems.
Angle Pairs
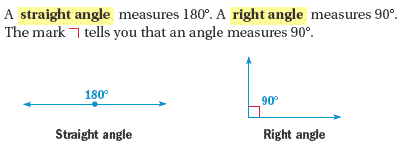
Two angles are supplementary if the sum of their measures is 180
.
Two angles are complementary if the sum of their measures is 90.
You can write "the measure of angle 1" as m∠1.
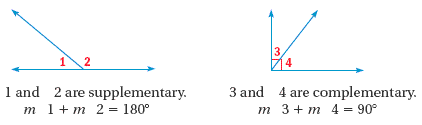
Example 1
∠1 and ∠2 are complementary, and m∠2 = 32°. Find m∠1.
Solution
m∠1 + m∠ 2 = 90° Definition of complementary angles
Vertical Angles
When two lines intersect at a point, they form two pairs of angles that do not share a side. These pairs are called vertical angles, and they always have the same measure.
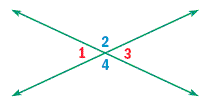
∠1 and ∠3 are vertical angles.
m∠1 = m∠3
∠2 and ∠4 are vertical angles.
m∠2 = m∠4
Perpendicular Lines
When two lines intersect to form one right angle, they form four right angles. Two lines that intersect at a right angle are called perpendicular lines.
Example 2
Find m∠2, m∠3, and m∠4.
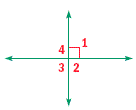
Solution
The diagram shows that m∠1 = 90°.
∠1 and ∠3 are vertical angles. Their measures are equal, so m∠3 = 90°.
∠1 and ∠2 are supplementary.
m∠1 + m∠2 = 180° Definition of supplementary angles
90° + m∠2 = 180° Substitute 90 for m∠1.
m∠2 = 90° Subtract 90 from each side.
∠2 and ∠4 are vertical angles. Their measures are equal, so m∠4 = 90°.
m∠2 = m∠3 = m∠4 = 90°
Parallel Lines
Two lines in the same plane that do not intersect are called parallel lines. When a third line intersects two parallel lines, several pairs of angles that are formed have equal measures.
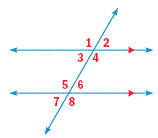
Corresponding Angles: m∠1 = m∠5; m∠2 = m∠6;
m∠3 = m∠7; m∠4 = m∠8
Alternate Interior Angles: m∠3 = m∠6; m∠4 = m∠5
Alternate Exterior Angles: m∠1 = m∠8; m∠2 = m∠7
Example 3
Use the diagram to find m∠1.
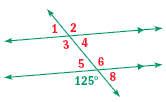
Solution
∠1 and ∠5 are corresponding angles, so they have equal measures.
Find m∠5. The angle with measure 125° and ∠5 are supplementary.
m∠5 + 125° = 180° Definition of supplementary angles
m∠5 = 55° Subtract 125° from each side.
∠1 and ∠5 have equal measures, therefore m∠1 = 55°.
Let's Practice Together
Are ∠1 and ∠2 are complementary, supplementary, or neither?
1. m∠1 = 79°
m∠2 = 101°
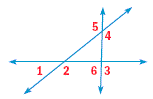
Find the measures of the numbered angles.
3.
Your Turn
Find the measures of the numbered angles.
4.
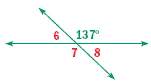
Find each angle measure.
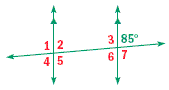
5. m∠2
6. m∠3
7. m∠4
8. m∠6
Complete the statement.
9. The sum of the measures of two _?_ angles is 180°.
10. Two lines that intersect to form a right angle are called _?_.
Are the angles complementary, supplementary, or neither?
11. m∠1 = 95°, m∠2 = 85°
12. m∠1 = 52°, m∠2 = 38°
13. m∠1 = 62°, m∠2 = 118°
14. m∠1 = 51°, m∠2 = 39°
Describe and correct the error in the solution.
15.
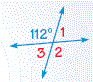
m∠2 = 68°, because vertical angles add up to 180°.
Check for Understanding
Find the value of the variable and the angle measures.
1. m∠1= (5x + 15)° and m∠2 = 28x°
2. m∠4 = (7n + 39)° and m∠5 = (11n − 13)°
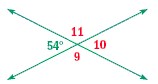
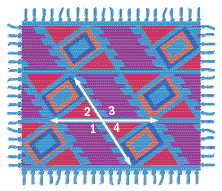
3. Find the angle measures in the weaving if m∠1 = 122°.
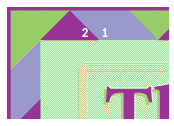
4. A student designed the stationery border shown here. Explain how to find m∠2 if m∠1 = 135°.
Answers
1. supplementary
2. neither
3. m∠9 = 126o; m∠10 = 54o; m∠11 = 126o
4. m∠6 = 43o; m∠7 = 137o; m∠8 = 43o
5. 85o
6. 95o
7. 85o
8. 85o
9. supplementary
10. perpendicular
11. supplementary
12. complementary
13. supplementary
14. complementary
15. Vertical angles are congruent, so m∠2 = 112o.
Check for Understanding
1. 5
2. 13
3. m∠2 = 58o; m∠3 = 122o; m∠4 = 58o
4. Angles 1 and 2 form a linear pair and are supplementary. So to find m∠2, subtract m∠1 from 180o. m∠2 = 180o - 135o = 45o.