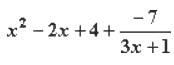---

There are two ways to divide polynomials.  One is to write the division in rational form, factor the polynomials, and then cancel out any common factors: 

Example

Divide x² + 9x + 14 by x + 7.




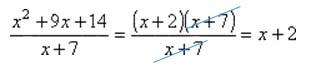
Polynomial Long Division (Synthetic Division)

Another option for dividing polynomials is to apply the process of long division.   Polynomial long division follows the same general steps as long division of conventional numbers.

It is important to write the polynomial in standard form, with exponents in descending order.  If any terms are missing in the polynomial, these terms are seen as the term multiplied by zero.  For instance, 4x³ + 2x + 1 would be rewritten as 4x³ + 0x² + 2x + 1 before dividing it by another term. In this example, the term 0x² is equal to zero, but it still needs to be taken into account in order to perform long division.


Example

Divide 3x³ - 5x² + 10x - 3 by 3x + 1



Explanation

To complete this division problem as shown above, consider the leading terms.

1. For the first step, consider what you need to multiply 3x by in order to obtain a product of 3x³.   The answer is x², which is written on the quotient line. 
2. Multiply x² by the divisor (3x + 1) and write the product down. 
3. Find the difference between the dividend and that product.
4. Bring down the next term.  

5. Consider what you can multiply the leading term, 3x, by in order to obtain a product of -6x². 
6. The answer is -2x, which is written on the quotient line. 
7. Multiply -2x by the divisor (3x + 1) and write the product down. 
8. Find the difference between the dividend and that product.
9. Bring down the next term.

+ Finally ...

10. Consider what you can multiply 3x by in order to obtain a product of 12x.
11. The answer is positive 4, so write +4 on the quotient line.
12. Multiply 4 by the divisor and write down the product.
13. Find the difference between the dividend and that product.

~ There are no more terms to bring down.~ 

14. The remainder is -7, which may be written as a fraction over the divisor.  Be sure to include this as an additional term in the polynomial.

Solution