Learning Target: I can compute the volume of a right rectangular prism with fractional side lengths.

Volume of Prisms with Fractional Lengths

The volume of a solid figure is a measure of the space enclosed by the figure. 

Volume is sometimes called capacity, and is measured in cubic units.

Volume tells us how many cubic units fit inside the space.

Example 1 

How many unit cubes will fit inside this box?

We can count 12 cubes on the front face of the box. (3 columns and 4 rows -- 3 × 4 = 12).

Then there are 4 stacks behind the front -- 5 stacks in all.

12 × 5 = 60

or (3 × 4) × 5 = 60

The volume of the solid is 60 cubic units.

Formula

The volume can be found by multiplying length × width × height.

Volume with Fractional Side Lengths

The same principles apply when the lengths of rectangular prisms are measured using unit fractions.

Example 2

Each of the following blocks measures ¹/₂ inch on a side.

How many cubic inches are in the volume of this box?

Like before, we can count 3 columns, 4 rows, and 4 stacks of cubes.  But each cube measures $\frac{1}{2}$ an inch, not a whole inch.  To find the measurement, we have to count the cubes by halves:

In this example, there are 4 half-inch cubes along the height ($\frac{4}{2}$ = 2 inches total); 3 half-inch cubes along the width ($\frac{3}{2}$ inches total); and 4 half-inch cubes along the depth ($\frac{4}{2}$ = 2 inches total).

Using the formula for volume:

V = l × w × h

V = 2 × $\frac{3}{2}$ × 2 = $\frac{2\times 3\times 2}{2}$ = $\frac{12}{2}$ = 6

The volume of the box is 6 cubic inches.

Example 3

Find the volume of this prism.

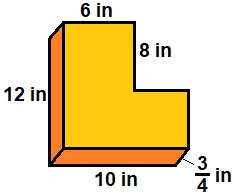
Although the shape is irregular, we can still use the usual formula to figure out its volume.  The shape can be split into two rectangular prisms.  Use the given measurements to figure out any missing ones.

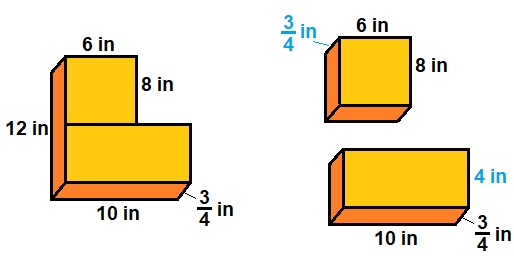
Top prism:  6 × 8 × $\frac{3}{4}$ = $\frac{144}{4}$ = 36 cubic inches

Bottom prism:  10 × 4 × $\frac{3}{4}$ = $\frac{120}{4}$ = 30 cubic inches

Total volume:  36 + 30 = 66

The volume of the prism is 66 cubic inches.

Let's Practice Together

1.    Find the volume of the rectangular prism.

Your Turn

2.   How many half-inch cubes could be combined to form a rectangular prism with a volume of 1 cubic inch?

A.  1

B.  2

C.  4

D.  8

A type of potting mix is condensed into cubes that measure $\frac{1}{2}$ cm on each side. 

The soil cubes are then packed into a box that measures 4 cm × 2$\frac{1}{2}$ cm × 3 cm.  The first layer of the box is packed, shown below.

3a.  What is the total volume of the box in cubic centimeters?

3b.  How many soil cubes measuring $\frac{1}{2}$ cm × $\frac{1}{2}$ cm will fit into the box if it is packed completely without any air gaps?

Check for Understanding

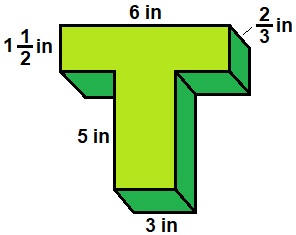
1.  Find the volume of the prism.

Answers

1.  $\frac{1}{24}$ m³

2.  D

3a.  30 cubic centimeters

3b.  240 cubes fit in the box. 

• The length will have 8 cubes.  (4 cm ÷ $\frac{1}{2}$ cm = 8.)
  
• The width will have 5 cubes.  (2$\frac{1}{2}$ cm ÷ $\frac{1}{2}$ cm = 5.)
  
• The height will have 6 cubes.  (3 cm ÷ $\frac{1}{2}$ cm = 6.)

       8 × 5 × 6 = 240

Check for Understanding

1.  16 cubic inches