Learning Target: I can identify and describe types of geometric transformations using ordered pairs in a coordinate plane.
Transformations With Coordinates
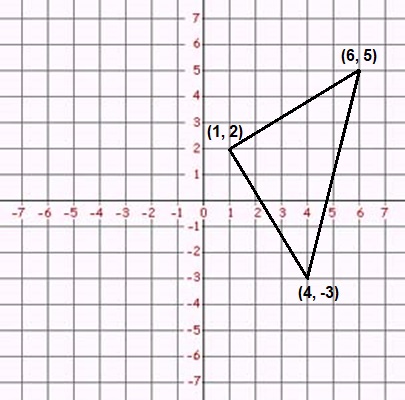
Coordinate planes are often used when sketching figures so their sizes and locations can be established.
If you need to move or resize part of the sketch, it's important to do that consistently, or the shape may end up unpleasantly distorted. Coordinate geometry can help with this.
The common transformations for geometric figures are translations, reflections, rotations, and dilations.
A translation is a change of position. You can perform a translation on a coordinate plane by adding/subtracting the same number to each of the x-coordinates, and each of the y-coordinates.
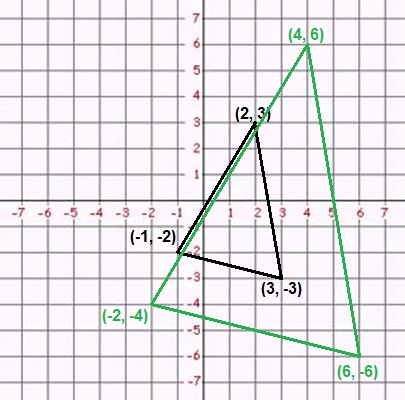
For example, in the triangle above, we can translate it 5 units to the left and 2 units upward. We can do this by replacing every point (x, y) with (x − 5, y + 2).
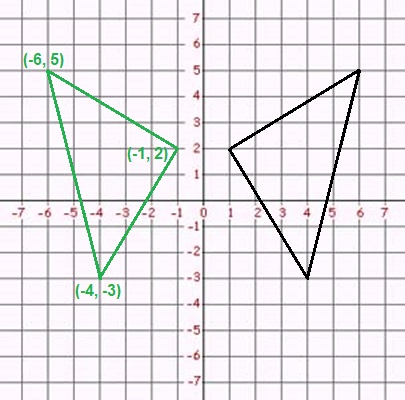
To perform a reflection, you need to change the sign of one of the coordinates for each point. If you want to reflect the figure over the y-axis, change the sign of each x-coordinate, so every (x, y) becomes (−x, y):
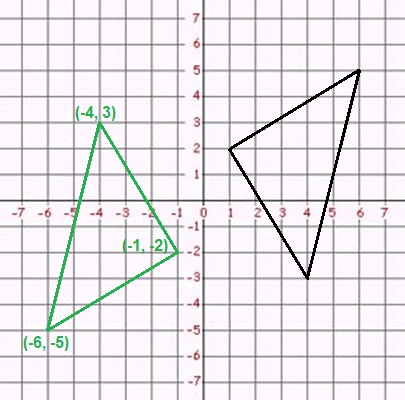
To reflect the figure over the x-axis, change the sign of the y-coordinate so every (x, y) becomes (x, −y):
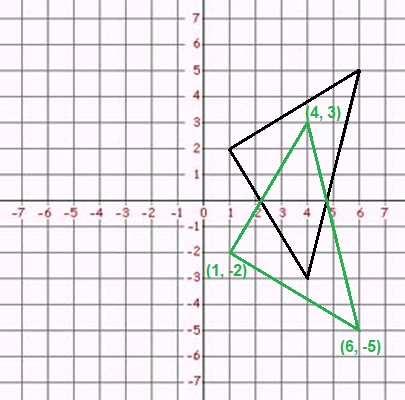
A rotation 180° around the origin is done by changing the signs of both coordinates, so every (x, y) becomes (−x, −y):
Notice how the translation, reflection, and rotation don't affect the size of the figure. This is important if you want to change the location of a structure or picture without changing its overall makeup. However, if you want to resize the figure, this is done using a dilation.
To perform a dilation, multiply or divide every coordinate by the same number. For example, if you wanted to increase the dimensions of a shape by a factor of two, multiply every coordinate by 2:
Notice how the lengths of the sides doubled, but the area of the shape actually quadrupled. This is because area is a two-dimensional measurement. If you multiply each dimension length by k, turning every coordinate (x, y) into (kx, ky), the area actually will be multiplied by k2.
Let's Practice Together
1a.) A figure on a grid is shifted 3 units to the left, 6 units upward, 5 units to the right, and 11 units downward. Use coordinates to describe the figure's current location relative to its original location.
1b.) The center of this figure is located at (-8, -3). Where would the center be if the figure were reflected over the x-axis?
Your Turn
2.) Consider the point (7, -4).
a.) Where would the point be if it were translated 6 units to the right and 3 units up?
b.) Where would the point be if it were reflected over the x-axis?
c.) Where would the point be if it were reflected over the y-axis?
d.) Where would the point be if it were rotated 180° around the origin?
3.) A figure on the grid is dilated by a factor of 3.
a.) If one of the figure's vertices were originally located at (-2, 5), where is the point after the dilation?
b.) If the area of the figure was originally 18, what is the area after the dilation?
Check for Understanding
1.) A segment with endpoints at (7, 9) and (-2, 3) is reflected over the y-axis and then translated 5 units downward. Find the endpoints of the new segment.
Answers
1a.) (x + 2, y − 5)
1b.) (-8, 3)
2a.) (10, 2)
2b.) (7, 4)
2c.) (-7, -4)
2d.) (-7, 4)
3a.) (-6, 15)
3b.) 162
Check for Understanding
1.) (-7, 4) and (2, -2)
