Finding Slope of a Line

The slope of a line is its steepness.  It can be determined by dividing the vertical change, called the rise, by the horizontal change, called the run.

Example

 

 

The greater the slope, the steeper the incline.  For example, a rise of 30 feet over a run of 60 feet would be steeper than the incline shown above, because 30/60 = 1/2, and 1/2 > 2/5.


Another definition of the slope of a line is the ratio of the vertical change to the horizontal change between any two selected points on the line.

 

The slope is consistent throughout the line.  In other words, it doesn't matter which two points you select, you will get the same slope every time.


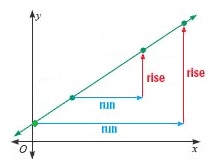
Because the triangles are similar, the rise/run ratios are the same, so the slopes will be equal.

 

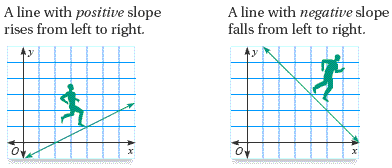
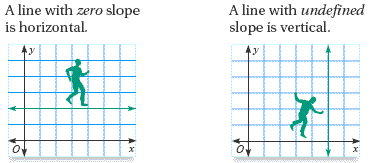
Types of slopes


 

 

Example

Find the slope of the line.

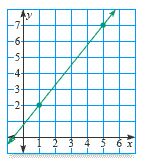
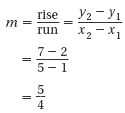
The slope is  5/4 .

 

 

 

Practice

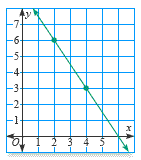
1)    Find the slope of the line shown.

 

 

 

 

 

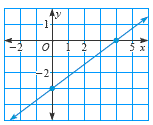
2)     What is the slope of the line shown in the graph?

 

 

 

 

 

 

 

3)    A line passes through the points (10, 0) and (x, -5) and has a slope of 1/2.

What is the value of x?

A.  -20
B.  -5
C.  0
D.  5

 

 

 

 

 

 

 

 

4)   Find the slope of the line passing through the points.

(-3, -4), (5, 2)

 

 

 

 

 

5)   Find the slope of the line passing through the points.

 (0, 6), (10, 0)

 

 

 

 

 

 

6)    Use the red line on the diagram of a birdhouse.

 

 

 

 

 

 

 

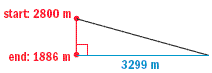
7)    A ski slope has a starting altitude of 2800 meters and an ending altitude of 1886 meters. The length of the ski slope is about 3299 meters. What is the approximate slope of the ski slope?  Round to the nearest hundredth.  

 

 

 

 

 

 





Answers

1.  -3/2

2.  3/4

3.  C

4.  3/4

5.  -3/5

6.  3;  3;  1

7.  -0.28