Angles and Triangles
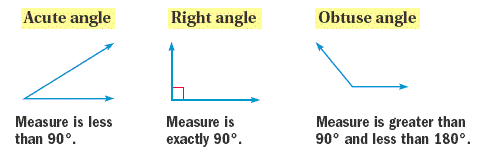
Classifying Angles

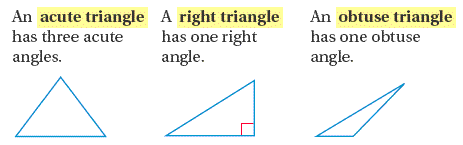
Classifying Triangles by Angles
Classifying Triangles By Sides
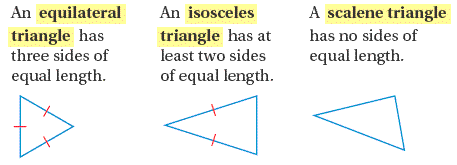
Example: Classifying a Triangle
Classify the triangle by its side lengths.
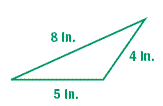
The triangle has no sides of equal length. So, it is a scalene triangle.
Example: Classifying a Triangle
Classify the triangle by its angles and by its side lengths.
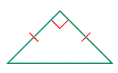
The triangle has one right angle and two sides of equal length. So, it is a right isosceles triangle.
Remember that the sum of the angle measures in the triangle is 180o. This is true for all triangles.
Finding an Unknown Angle Measure
Find the value of x and then classify the triangle by its angles.
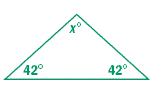
Solution
The sum of the angle measures in a triangle is 180 degrees.

The triangle has one obtuse angle, so it is an obtuse triangle.
Practice
Find the value of x and then classify the triangle by its angles.
1
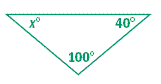
2
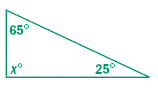
3 Complete the statement.
A(n) _?_ triangle has no sides of equal length.
4 Classify the triangle by its side lengths.
a.
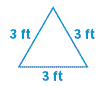
b.
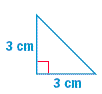
c.
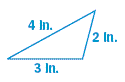
5 Describe and correct the error in the solution.

6 Estimation
The referee is making calls during a hockey game.
Classify the angle made by his arms as acute, obtuse, or right.

7 Find the value of x. Classify the triangle by its angles.
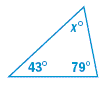
8 Can the angles in a triangle have the measures given? Explain.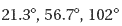
9 Find the value of x.
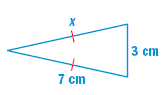
A. 3 cm
B. 4 cm
C. 7 cm
D. 10 cm
10 If the two side edges of this gable are the same length, what kind of triangle is formed? Explain.

Answers
1. 40o, obtuse
2. 90o, right
3. scalene
4a. equilateral
4b. isosceles
4c. scalene
5. An acute triangle has 3 acute angles, not just 1. The figure contains a right angle and is therefore a right triangle.
6. obtuse
7. 58o, acute
8. Yes, because the measures add up to 180o.
9. C
10. The triangle would be isosceles, because isosceles triangles have two sides the same length.