Heat and work in thermodynamic processes

A thermodynamic system has the potential to exchange energy with its surroundings by heat transfer or by mechanical work. When a system at pressure p changes volume from V₁ to V₂, it does an amount of work W given by the integral of p with respect to volume.

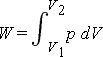
If the pressure is constant, the work done is equal to p times the change in volume. A negative value of W means that work is done on the system.

W = p(V₂ V₁)

In any thermodynamic process, the heat added to the system and the work done by the system depend not only on the initial and final states, but also on the path ( the series of intermediate states through which the system passes).

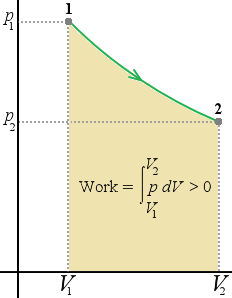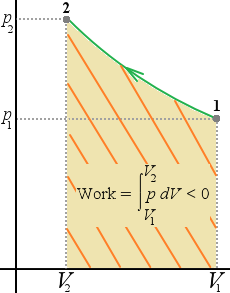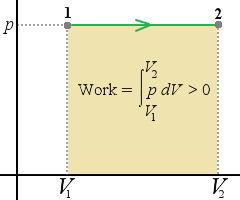pV-diagram for a system undergoing am expansion with varying pressure	pV-diagram for a system undergoing a compression with a varying pressure (The cross lines indicate negative work)	pV-diagram for a system undergoing an expansion with constant pressure

The work done equals the area under the curve on a pV-diagram

When a thermodynamic changes from initial to a final state it passes through a series of intermediate states called a path. When the states are in equilibrium the path can be plotted on a pV-diagram. In the plot below the work done by the system during a transition between two states, where we increase volume from V₁ to V₂ while decreasing the pressure from p₁ to p₂

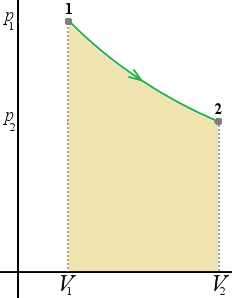
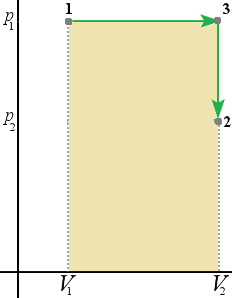
On the diagram below (1) first we decrease the pressure from p₁ to p₂ (3), then we decrease the volume from V₁ to V₂ (2).

On the diagram below (1) first we decrease the pressure from V₁ to V₂(4), then  we decrease the volume from p₁ to p₂ (2).

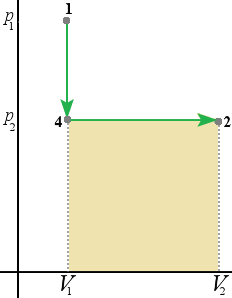
Since the area below the curve is the work done we can conclude that the work done by the system depends not only on the initial and final states but also the intermediate states.

The first law of thermodynamics states that when heat Q is added to a system while the system does work W, the internal energy U changes by an amount equal to Q -W. This law can also be expressed for an infinitesimal process.

U = Q W

dU = dQ dW

infinitesimal process

The internal energy of any thermodynamic system depends only on its state. The change in internal energy in any process depends only on the initial and final states, not on the path. The internal energy of an isolated system is constant. In a thermodynamic process, the internal energy U of a system may increase (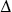U > 0), decrease (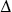U < 0) or remain the same (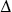U = 0)

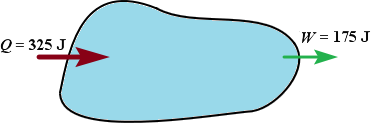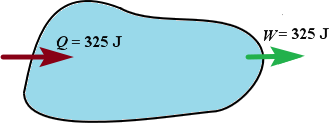More heat is added to the system than the system does work, the internal energy of the system increases	More heat is flows out of the system than the system does work, the internal energy of the system increases	Heat added to the system equals work, the internal energy is unchanged
U = Q W = +150J	U = Q W = 150J	U = Q W = 0

Important types of thermodynamic processes

• Adiabatic process: No heat transfer into or out of a system; Q =0.

where = $\frac{C_p}{C_v}$

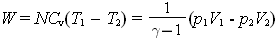
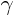• Isochoric process: Constant volume; W = 0.

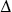U₂ - U₁ = U = Q

• Isobaric process: Constant pressure

W = p(V₂ - V₁)

• Isothermal process: Constant temperature

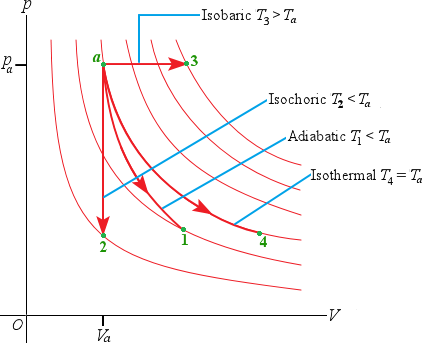Four different types of thermodynamic processes where there is a constant amount of an ideal gas. All processes start at state a.

Thermodynamics of ideal gases

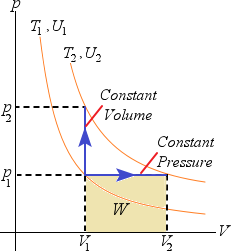
The internal energy of an ideal gas depends only on its temperature, not its pressure or volume. For other substances the internal energy generally depends on both pressure and temperature. The molar heat capacities C_v and C_p of an ideal gas differ by R, the ideal gas constant. The dimensionless ratio of heat capacities, C_p/ C_v is denoted by .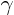

C_p = C_v + R

Increasing the temperature of an ideal has from T₁ to T₂ by a constant pressure the gas does work:

Q = 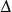U + W, since more heat must be added to increase both U and do work W.

When it is increased at a constant volume the gas does no work, therefore Q = 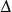U

Adiabatic processes in ideal gases

For an adiabatic process for an ideal gas, the quantities

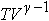
and

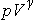
are constant. The work done by an ideal gas during an adiabatic expansion can be expressed in terms of the initial and final values of temperature, or in terms of the initial and final values of pressure and volume.

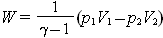
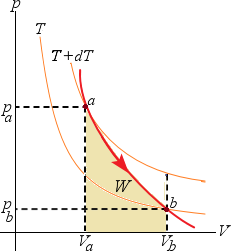
Adiabatic process as a goes to b. As the gas expands from V_a to V_b, it does positive work W on its environment,

the gas internal energy decreases (U = W and U < 0) and the temperature drops from T + dT to T.

1. A quantity of ideal gas undergoes an expansion that increases its volume from V₁ to V₂ = 2V₁. The final pressure of the gas is p₂. Does the gas do more work on its surroundings if the expansion is at constant pressure or at constant temperature?

(i) constant pressure

(ii) constant temperature

(iii) the same amount of work is done in both cases

(iv) not enough information is given to decide.

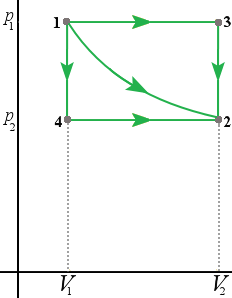
2 . The system described in the figure above undergoes four different thermodynamic processes. Each process is represented in a pV-diagram as a straight line from the initial state to the final state. Rank the processes in order of the amount of work done by the system, from the most positive to the most negative.

(i) 1 2

(ii) 2 1

(iii) 3 4

(iv) 4 3

3. Rank the following thermodynamic processes according to the change in internal energy in each process, from most positive to most negative.

(i) As you do 250 J of work on a system, it transfers 250 J of heat to its surroundings.

(ii) as you do 250 J of work on a system, it absorbs 250 J of heat from its surroundings.

(iii) as a system does 250 J of work on you, it transfers 250 J of heat to its surroundings.

(iv) as a system does 250 J of work on you, it absorbs 250 J of heat from its surroundings.

4. Which of the processes are isochoric? Which are isobaric? Is it possible to tell if any of the processes are isothermal or adiabatic?

5. Is the internal energy of a solid likely to be independent of its volume, as is the case for an ideal gas? Explain your reasoning.

6. You want to cool a storage cylinder containing 10 moles of compressed gas from 30C to 20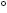C. For which kind of gas would this be easiest?

(i) a monatomic gas

(ii) a diatomic gas

(iii) a polyatomic gas

(iv) it would be equally easy for all of these