Calculus is the study of motion and change, which is done most easily when the motion is smooth and unbroken. So the first thing to understand in this subject is how exactly to define smooth, unbroken motion. We call this kind of motion continuity, or continuous motion.

One way to recognize continuous motion is simply by looking at a graph. Often, if the curve appears to show fluid movement without any holes or jumps, it represents continuous motion. In other words, the function that created it is a continuous function.

But appearances can be deceiving. Even a curve that looks as smooth as silk could have a break or two if you zoom in closely enough. So how can you tell if a function actually is continuous or not?

We can determine continuity by taking a limit. A limit is a way of figuring out what value a function is approaching. If the function is approaching the value we expect it to at a certain point, then the function is continuous there.

To answer this question, we need to look at x-values that are close to 4, but not 4 itself. We can plug in a whole bunch of values and put them on a table for easy viewing:

Notice that we’re approaching 4 from both sides. That’s important-- there’s always a chance that one side will tell a different story from the other. But we can see that in this case, both f(x) columns are approaching 15. If we continued and plugged in numbers even closer to 4 (i.e., 3.99999, 4.000001), we would get function values even closer to 15.

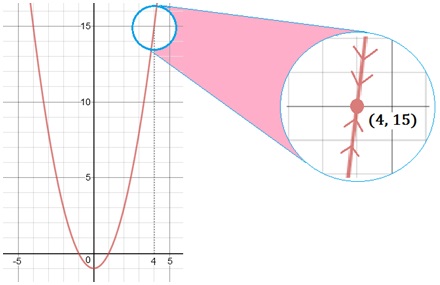
The graph of f(x) = x² − 1 supports our conclusion; both sides are clearly approaching the y-value of 15. We now have all the evidence we need.

The “lim,” as you’ve probably guessed, stands for “limit,” and the “x → 4” underneath it tells us where x is going.

Because the limit as x goes to 4 of f(x) [that is,

\lim_{x \to 4}

f(x)] happens to be the same as f(4), we can now officially say the function f(x) = x² − 1 is continuous at x = 4.

\lim_{x \to c}

f(x) = f(c), provided the values exist, then f(x) is continuous at c.

Continuous function values are going to prove very important as we explore the topics of calculus.

Here’s a tip: Polynomial, rational, exponential, logarithmic, and trigonometric functions are all continuous at every point where they’re defined. That should save you a heap of trouble.

Since x³ + 4x is a polynomial function, it’s continuous everywhere. You can find the limit simply by plugging in the number.

Limits are pretty easy to define from a conceptual standpoint. Sometimes, though, you might encounter a more formal definition of the limit. So for all you fancy types out there, here's another look at the concept:

If, for every ε > 0, you can find a δ > 0 so that |f(x) − L| < ε as long as |x − a| < δ, then

\lim_{x \to a}

f(x) = L.

What all this math-speak is trying to say is that if you pick any small value for epsilon (the little "ε" thing), let's say 0.001 for example, you can find a neighborhood of x-values surrounding your a where the values of f(x) all come within 0.001 of the limit L.

Let's try this out with f(x) = 5x − 3 and a = 1. It's pretty obvious the limit here is going to equal 2, but let's justify that formally:

There you have it. Pick an epsilon, divide it by 5, and you've got the delta (the fancy "δ" thing) you need to satisfy the inequalities. If you pick ε = 0.01, then δ = ^0.01/₅ = 0.002; this means the value of f(x) will fall within 0.01 of 2 (that is, between 1.99 and 2.01) when the x-value lies within 0.002 of 1 (that is, between 0.998 and 1.002). We have just proven

\lim_{x \to 1}

(5x − 3) = 2.

4. Use the formal definition of the limit to prove

\lim_{x \to 4} (9 - 2 x) = 1

x	*f(x)*	x	*f(x)*
3.5	11.25	4.5	19.25
3.9	14.21	4.1	15.81
3.95	14.6025	4.05	15.4025
3.99	14.9201	4.01	15.0801
3.999	14.992001	4.001	15.008001