 Learning Target: I can identify a function and describe the relationship based on a set of ordered pairs.
Learning Target: I can identify a function and describe the relationship based on a set of ordered pairs. Learning Target: I can identify a function and describe the relationship based on a set of ordered pairs.
Learning Target: I can identify a function and describe the relationship based on a set of ordered pairs.
Relations and Functions
A relation is a set of ordered pairs that relates an input to an output. A relation can be written as a set of ordered pairs or by using an input-output table.
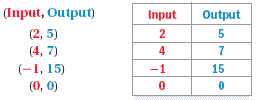
A relation is a function if for each input there is exactly one output. In a function, you can say that the output is a function of the input.
Identifying Functions
Tell whether the relation is a function. Explain your answer.
Example 1
(0, 2), (1, 4), (2, 6), (3, 8)
The relation is a a function. Each input has exactly one output.
Example 2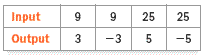
The relation is not a function. Both 9 and 25 have two outputs.
The domain of a function is the set of all possible input values. The range of a function is the set of all possible output values. A function rule assigns each number in the domain to exactly one number in the range.
Example 3
Your school baseball team is selling glow sticks to raise money. The team paid $50 for a case of 48 glow sticks and sells each glow stick for $3. How many glow sticks does the team need to sell to start earning a profit?
To solve the problem, use the function rule P = 3g - 50, where P is the profit in dollars and g is the number of glow sticks your team sells.
Make a table to determine how many glow sticks your soccer team needs to sell to start earning a profit.

There are 48 glow sticks, so the domain is 0, 1, 2, 3, . . . , 48. The range is -50, -47,-44, -41, . . . , 94.
Your baseball team needs to sell at least 17 glow sticks.
Writing a Function Rule
Example 4
Write a function rule that relates x and y.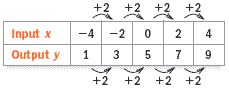
To write a function rule, try to find an equation of the form y = ax + b. You can look at differences in the function to find values of a and b.
Step 1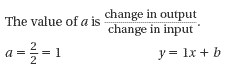
Step 2
To find b, choose an input-output pair to substitute for x and y.
Let (x, y) = (0, 5)
5 = 1(0) + b, so b = 5
A function rule that relates x and y is y = x + 5.
Check: 3 = -2 + 5 Substitute (-2, 3) in function rule.
Let's Practice Together
Tell whether the relation is a function.
1) (-2, 4), (2, 4), (4, 2), (-2, -4)
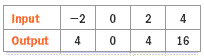
2) Tell whether the relation is a function.
Your Turn
3) Complete the statement: A function has exactly one output value for each _?_.
4) The function rule y = 3x relates x and y in which set of ordered pairs?
A (0, 0), (3, 1), (6, 2), (9, 3)
B (0, 0), (1, 3), (2, 6), (3, 9)
C (0, 3), (1, 4), (2, 5), (3, 6)
D (0, -3), (1, -2), (2, -1), (3, 0)
5) Which of the following relations is not a function?
A (2, 3), (4, 3), (6, 7), (9, 2)
B (2, 3), (4, 5), (6, 4), (5, 4)
C (-1, 8), (0, 11), (1, 8), (5, 4)
D (3, 5), (4, 3), (4, 6), (6, 9)
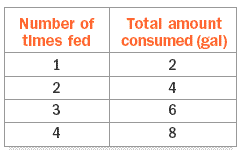
6) A whale is fed a milk based formula. The table shows the amounts of formula, in gallons, the whale drinks every 3 to 4 hours. Use the table to write a function rule.
7) Tell whether the relation is a function.
(3, 0), (0, 6), (1, 5), (3, 7) (-1, 2), (5, 1), (-3, 0)
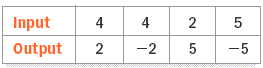
8) Tell whether the relation is a function.
Check for Understanding
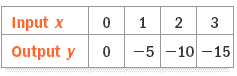
1) Write a function rule that relates x and y.
2) Complete the table of values for the function rule.
5x + y = 13

Answers
1. no
2. yes
3. input
4. B
5. D
6. a = 2n
7. no
8. no
Check for Understanding
1. y = -5x
2. 18, 13, 8, 3