Comparing Function Behaviors
A function is a rule that takes an input value and generates exactly one output value. When you do this enough times, you usually start seeing a pattern in the values.
Looking at the numbers, you can see the output values go up by 3 each time. Continuing the pattern, we can conclude that the output value for 5 must be 20, and the output for 6 must be 23.
Different functions generate different patterns, and you can often compare one with another. Look at this example:
Again looking at the differences, we see the output values go up by 2, then by 4, then by 6. Following this pattern, we can conclude that the output for 5 must be 25 (eight more than 17), and the output for 6 must be 35 (ten more than 25).
Notice some interesting relationships between these two functions. In both cases, the output values are increasing, but they're not increasing at the same rate. Also, the first three input values give greater output values in the first function, but when the input value is 4, both functions have the same output. After that, the second function's output values are greater (and will continue to be greater for as long as you want to extend the tables).
You can also compare functions algebraically.
An equation like y = x + 3 can represent a function. Any value you pick for x will give you exactly one value for y. For example, if x = 1, then y must be 1 + 3 = 4. If x = 5, then y must be 5 + 3 = 8. There are no other possibilities for y for each possible x.
Another example of an algebraic function is y = 3x. This may look similar, but if you look for values here, you'll find that they're quite different. If x = 1, then y will be 3 × 1 = 3. If x = 5, then y = 3 × 5 = 15. Notice how when x = 1, the function y = x + 1 has the greater value. But when x = 5, y = 3x has the greater value. However, both functions produce increasing y values when the value of x increases.
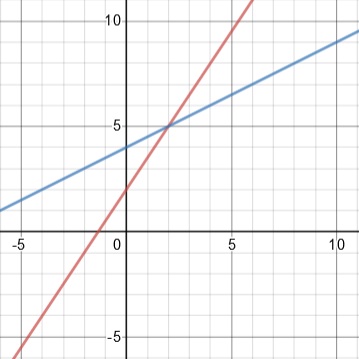
You can compare functions graphically.
You can graph functions by plotting ordered pairs (x, y), where y is the output value generated by the x-value.
Here's an example of two functions graphed together:
Notice how, once again, both functions increase as the x-values increase. The blue function has the greater values until the x-value of 2, then the red function produces the greater values.
Practice
1.) Compare the two functions.
| Input | 1 | 2 | 3 | 4 | 5 | 6 |
| Output | 8 | 10 | 12 | 14 | 16 | ... |
| Input | 1 | 2 | 3 | 4 | 5 | 6 |
| Output | 1 | 4 | 7 | 10 | 13 | ... |
If the patterns continue, what input value will yield the same output value for both functions?
2.) Compare the functions defined by the equations y = 4x − 1 and y = 7 + 3x. If x increases at the same rate for both functions, for which equation will the y-values increase at a faster rate?
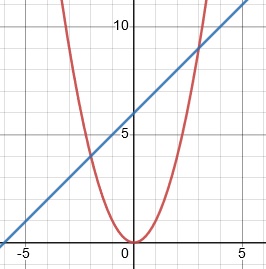
3.) Compare the functions graphed simultaneously below.
For what range of x-values are the function values defined by the red curve less than the function values defined by the blue line?
Answers
1.) 8
2.) y = 4x − 1
3.) between -2 and 3