Right Triangle Relationships

---

Right triangles are often used when finding locations because a direct, slanted distance can be expressed in terms of easily measured horizontal and vertical distances.

The Pythagorean Theorem shows how the hypotenuse, c, of a right triangle is related to its legs, a and b.

Given one of the sides and the hypotenuse, the other side can be found by solving for either a or b.

---

Example

A government agency decides to build a memorial park in the shape of a right triangle. They decide that the longest side will be 30 yards longer than 3 times the length of the shortest side. If the hypotenuse will be 15 yards longer than the longest side, what are the sides of the triangle?

Let x be the length of the shortest leg, so if we use the a, b, and c notation we have

where b is the length of the longest leg.

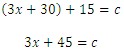
where c is the length of the hypotenuse. Let us write the equation now and then solve for x.

 

 

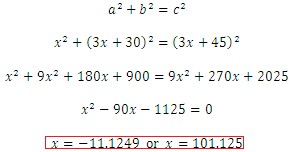
Does it make sense? Since the sides of the triangle represent a length, an answer of -11.1249 does not seem reasonable. So, using our second value we find that

---

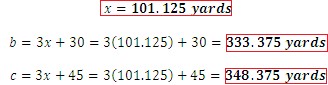
Ratios to Remember

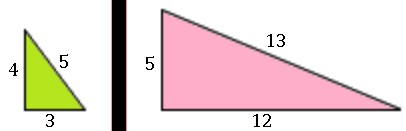
There are several examples of right triangles, but there are two common ratios for side a: side b: side c. One example is the 3-4-5 triangle:

length of side a : length of side b: length of side c = 3:4:5

Another one of these relationships is the 5-12-13 triangles. You can use the Pythagorean Theorem to test these relationships.

 

---

Special Triangles

Right triangles with angles that measure 45^o- 45^o- 90^o or 30^o- 60^o- 90^o are called special right triangles. They obey the theorems below.

---

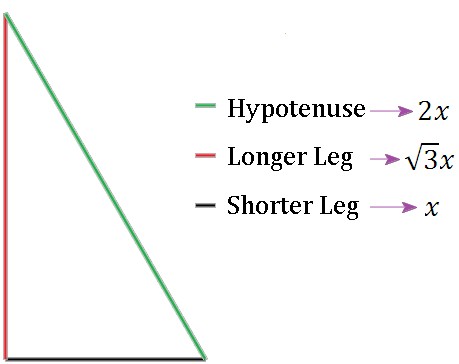
30^o- 60^o- 90^o Triangle Theorem

 

In a triangle that has the angles 30, 60, and 90 degrees, the hypotenuse is 2 times as long as the shorter leg, and the longer leg is  times as long as the shorter leg.

 

---

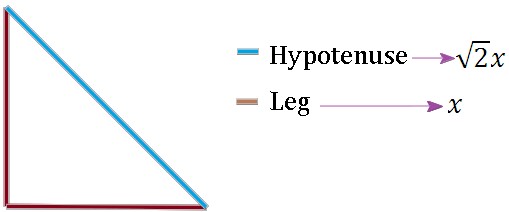
45^o-45^o-90^o Triangle Theorem

In a triangle with the angles 45^o, 45^o, and 90^o, the hypotenuse is  times as long as each leg.

 

 

---

Example

Find the length of side L and hypotenuse H: 

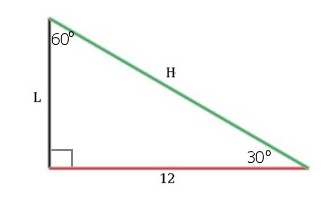
Because the triangle has 30-, 60-, and 90-degree angles,

we can use the 30^o-60^o-90^o Triangle Theorem. 

                 

           

---

Example

Find the length of s in the following triangle:

 

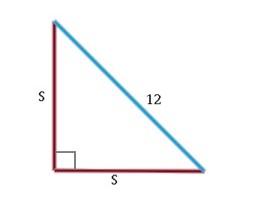
Because this shape is a right triangle, and the two sides have the same length, s, it must be a 45^o- 45^o- 90^o triangle. So, we can use that theorem to solve for s.

---

Guided Practice

 

1. Stage Height

 

 a. A rock band uses a ramp at a theater to load and unload the equipment from the main stage. If the ramp is 20 meters long and has an incline of 30 degrees, how high is the main stage?

 

 

b. How high is the main stage if the ramp has an incline of 60 degrees?

 

c. How high is the main stage if the ramp has an incline of 45 degrees?

 

 

 

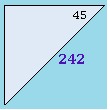
2. Find the unknown lengths of the sides in the triangles below:

 

 

a. What is the length of the hypotenuse?

 

 

 

 

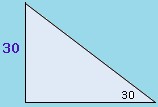
b. What is the height of this isosceles triangle?

 

 

 

c.What is the length of each leg?

Answers

1.  a. 10 m  b. m  c. m

2.  a. 60  b.   c.