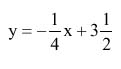Slope-Intercept Form
Slope-Intercept Form
An equation is in slope-intercept form, if it is in the form:
y = mx + b
The graph of the equation will always be a straight line with a slope of m and a y-intercept of (0, b).
Example 1
Determine the slope and y-intercept of the following line:
-4x + 2y = 16
Solution
Write the original equation in slope-intercept form by adding 4x to each side and then dividing everything by two:
-4x + 2y + 4x = 16 + 4x
(2y) ÷ 2 = (4x + 16) ÷ 2
y = 2x + 8
The slope is 2. The y-intercept is 8, or (0, 8).
You can also use the slope and y-intercept to graph a line.
Example 2
Graph the equation: y = 1/2x + 2
Solution
Using the slope-intercept form we see that the y-intercept is 2, so the first point is at (0, 2)
The slope is 1/2, so we can plot a second point by moving up 1 unit and then to the right 2 units.
Finally we draw a line through both points.
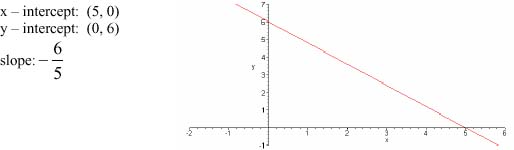
1. Find the x- and y-intercepts, slope and graph of 6x + 5y = 30.
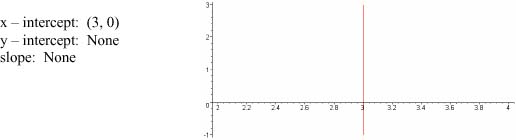
2. Find the x- and y-intercepts, slope and graph of x = 3.
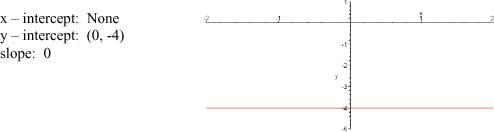
3. Find the x- and y-intercepts, slope and graph of y = -4.
4. Write in slope-intercept form the line that passes through the points (4, 6) and (−4, 2).
5. Write in slope-intercept form the line parallel to the graph of x + 4y = −1 and containing the point (2, 3). (Hint: Parallel lines have the same slope.)
Answers
1.
2.
3.
4. 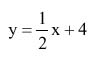
5.