Coordinate System (Parallel/Perpendicular/Intercepts)
Coordinate System
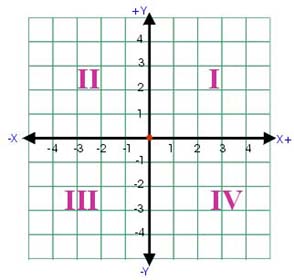
The coordinate system is a grid system, similar to a map. Its lines are formed by two axes that are drawn perpendicular to each other. The horizontal axis is called the x-axis, and the vertical axis is called the y-axis. The two intersecting axes form four quadrants, numbered I through IV.
The point of intersection (0, 0) is called the origin. In an ordered pair, the x-coordinate is always listed first and the y-coordinate second.
Intercept
Example 1
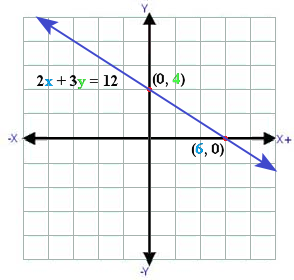
The y-intercept is 4
The x-intercept is 6
- The graph of 2x + 3y = 12 crosses the x-axis at (6, 0), so its x-intercept is 6.
- The graph of 2x + 3y = 12 crosses the y-axis at (0, 4), so its y-intercept is 4.
Example 2
Find the intercepts of the graph
y = x − 5
To find the x-intercept, let y = 0 and solve for x:
0 = x − 5
5 = x
10 = x
y = (0) − 5
y = 0 − 5
y = −5
The x-intercept is 10, and the y-intercept is −5.
The graph of the equation contains the points (10, 0) and (0, −5). You could plot these two points and connect them to determine the graph of the line.
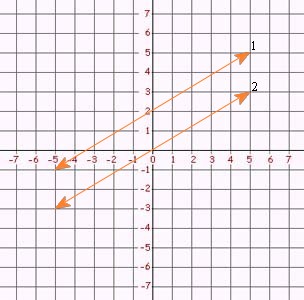
Compare the Slopes of Lines
Consider two different non-vertical lines 1 and 2. Line 1 has a slope m1, and line 2 has a slope m2. The lines are parallel if and only if they have the same slope:
m1 = m2
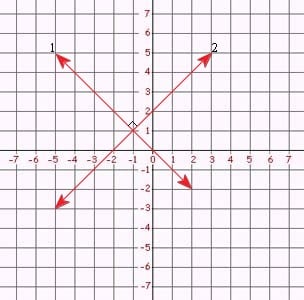
The lines are perpendicular if their slopes are negative reciprocals of each other. Therefore, perpendicular lines have the following relationships between their slopes:
or
Practice
1. Determine the quadrant for the following points.
a. (4, −1) b. (−2, −8) c. (−9, 3)
2. Find the x- and y-intercepts for the graph of the equation 6x − 2y = 24.
3. Given the line y = x + 4, find the following.
a. the slope of a line parallel to its graph
b. the slope of a line perpendicular to its graph.
Answers
1. a. IV b. III c. II
2. x-intercept: 4, y-intercept: −12
3. a. b.