Learning Target: I can use the Pythagorean Theorem to solve problems and determine whether given side lengths form a right triangle.

---

Using the Pythagorean Theorem

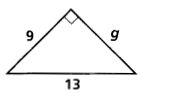
Find the value of g. Write your answer in simplest radical form.

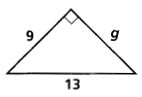
Using the Pythagorean Theorem, substitute g and 9 for the legs and 13 for the hypotenuse.

 

a² + b² = c²

 g² + 9² = 13²           Substitute

g² + 81 = 169           Simplify

        g² = 88             Subtract 81 from each side

        g² = $\sqrt{88}$         Take the square root

         g =  $2\sqrt{22}$      Simplify

 

You can simplify radicals by looking for square number factors.

$\sqrt{88}=\sqrt{4\times 22}=\sqrt{4}\times \sqrt{22}=2\sqrt{22}$

You can also use the Pythagorean Theorem in the other direction (that is, use the converse of the Pythagorean Theorem) to determine whether a triangle is right.

Example 2

Is a triangle with sides of lengths 8, 12, and 14 a right triangle?

If this is a right triangle, then the sides should follow the Pythagorean Theorem, with the longest side being the hypotenuse.
        a² + b² = c²

        8² + 12² ? 14²

        64 + 144 ? 196

        208 > 196

The theorem doesn't hold.  So the triangle is not a right triangle.

As a bonus, however, we can figure out what kind of triangle this is.

        If a² + b² > c², the triangle is acute.

        If a² + b² < c², the triangle is obtuse.

Because 208 > 196, the triangle is acute.

---

Let's Practice Together

Find the missing side lengths. Leave your answers in simplest radical form.

 

1. 

 

 

 

 

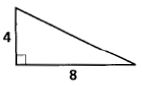
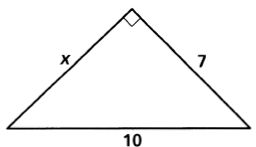
2.

3.  A triangle has side lengths of 12, 15, and 20.  Is this triangle acute, right or obtuse?

 

---

Your Turn

Find the missing side lengths.  Leave your answers in simplest radical form.

4.

 

 

 

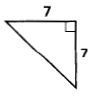
5.

 

 

 

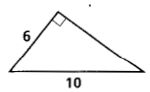
6.

 

 

 

 

 

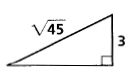
Find the value of each variable. Leave your answers in simplest radical form.

7.

 

 

 

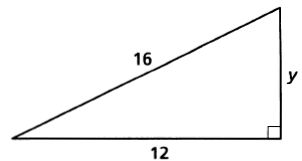
8.

 

 

 

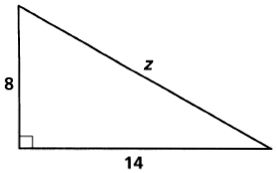
9.

 

 

 

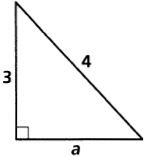
10.

 

 

 

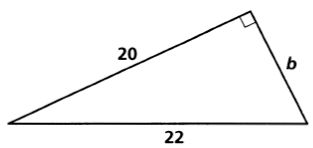
11.

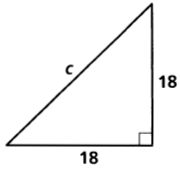
The numbers represent the lengths of the sides of a triangle. Classify each triangle as acute, obtuse, or right.

12.       6, 9, 10

 

 

 

13.       7, 24, 25

 

 

 

14.       18, 24, 30

 

 

 

15.       2, 5, 6

 

 

 

16.       20, 100, 110

 

 

 

17.       13, 21, 24

---

Check for Understanding

Find the area of each triangle. Leave your answers in simplest radical form.

 

1.

 

 

 

 

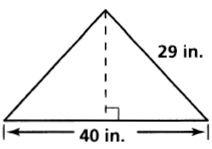
2.

 

 

 

 

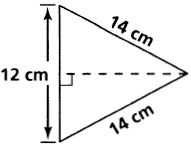
3.

 

 

 

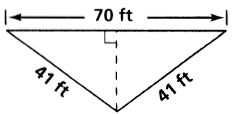
Answers

1.  $4\sqrt{5}$

2.  $\sqrt{51}$

3.  obtuse

4.  $7\sqrt{2}$

5.  8

6.  6

7.  $4\sqrt{7}$

8.  $2\sqrt{65}$

9.  $\sqrt{7}$

10.  $2\sqrt{21}$

11.  $18\sqrt{2}$

12.  acute

13.  right

14.  right

15.  obtuse

16.  obtuse

17.  acute

Check for Understanding

1.  420 in²

2.  $24\sqrt{10}$ cm²

3.  $70\sqrt{114}$ ft²