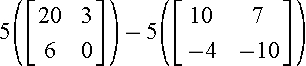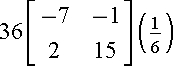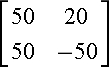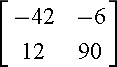Adding and Subracting Matrices
Matrix Operations
A matrix is often used to represent a series of operations, but you can perform operations on matrices themselves.
Addition and Subtraction
Addition and subtraction are rather straightforward with matrices, just add or subtract the corresponding elements.
Addition and subtraction can only be done if the matrices have the exact same order. In other words, both the number of rows and the number of columns has to be the same on both matrices.
cannot be done
Multiplication By Scalar
The product of a real number k, called a scalar, and a matrix M is a new matrix kM, where kM stands for the multiplication of all the elements of matrix M by scalar k.
Example
Multiply the scalar 5 by the matrix .
Solution
Properties of Scalar Multiplication
Let M and N be matrices of the same order, and let m and n be scalars. The following are the properties of scalar multiplication:
- Associative Property → (mn)M = m(nM)
- Distributive Property → (m + n)M = mM + nM
- Distributive Property → m(M + N) = mM + mN
- Scalar Identity → 1M = M
- Scalar Commutative Property → m(M)n = mn(M)
Exercises
Perform the following operations if possible.
1.)
2.)
3.)
4.)
5.)
Answer Key
1.)
2.) not possible
3.)
4.)
5.)