Angles in the Plane

Angles in the Plane

Below is a summary of the basic facts about the angles formed in a plane by lines, line segments, and rays.

Vertical angles and supplementary angles. Two opposite angles formed by two intersecting lines are called vertical angles.

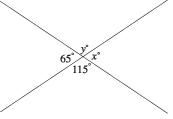
Vertical angles have the same measure. In the figure above, y = 115° and x = 65°.

Note that any pair of angles next to each other in the figure have measures that add up to 180°. (This is the measure of a straight angle: the angle formed by a straight line.) Two angles whose measures have a sum of 180° are called supplementary angles.

Parallel lines. When a line intersects a pair of parallel lines, the eight angles formed are related in several ways.

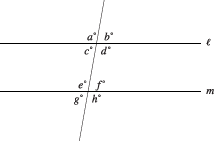
The measures of corresponding angles are equal; for example, a and e are equal, as are d and h. Also, several pairs of angles each add up to a straight angle; for example, d + f = 180° and a + g = 180°. Finally, alternate interior angles have equal measures; in the figure, c and f are equal, as are d and e.

Right angles: A right angle is an angle with a measure of 90°.
Perpendicular lines: If two lines intersect and one of the four angles formed is a right angle, the lines are perpendicular. In this case, all four angles that are formed are right angles.
Complementary angles: Two angles whose measures have a sum of 90° are called complementary angles.