Permutations and Combinations
Permutations


Factorials!In the last example, you evaluated 5 × 4 × 3 × 2 × 1. When you multiply a number by the number 1 less than itself, then by the number 1 less than that, and so on, all the way down to 1, this is known as a factorial. You can write "5 × 4 × 3 × 2 × 1" as "5!" which is read as "5 factorial."5! = 5 × 4 × 3 × 2 × 1n! = n × (n − 1) × (n − 2) × ... × 1Note: The value of 0! is defined as 1.


***
A combination, on the other hand, is a group of items whose order is not important. For example, suppose you go to lunch with a friend. You choose milk, soup, and a salad. Your friend chooses soup, a salad, and milk. The order in which the items are chosen does not matter. You both have same meal.
Listing Combinations
Example
You have 4 tickets to the county fair and can take 3 of your friends. You can choose from Abby (A), Brian (B), Chloe (C), and David (D). How many different choices of groups of friends do you have?
Solution
List all possible arrangements of three friends. Then cross out any duplicate groupings that represent the same group of friends.

You have 4 different choices of groups to take to the fair.
Combination Notation
In Example 1, after you cross out the duplicate groupings, you are left with the number of combinations of 4 items chosen 3 at a time. Using notation, this is written 4C3.
To find the number of combinations of n objects taken r at a time, divide the number of permutations of n objects taken r at a time by r !.
Formula: Example: 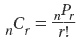
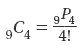
Evaluating Combinations
Find the number of combinations if you select 3 items from a group of 8.
8C3


Distinguishing Permutations and Combinations
Examples
State whether the possibilities can be counted using a permutation or combination. Then write an expression for the number of possibilities.
a. There are 8 swimmers in the 400 meter freestyle race. In how many ways can the swimmers finish first, second, and third?
Solution: Because the swimmers can finish first, second, or third, order is important. So the possibilities can be counted by evaluating 8P3.
b. Your track team has 6 runners available for the 4-person relay event. How many different 4-person teams can be chosen?
Solution: Order is not important in choosing the team members, so the possibilities can be counted by evaluating 6C4.